Wskaźniki zdolności są ważnym elementem w zarządzaniu jakością procesów, jednak używane bez należytej uwagi mogą spowodować chaos i dostarczyć nieprawdziwych informacji.
Wykorzystywane w ramach statystycznego sterowania procesami karty kontrolne są bardzo dobrym narzędziem do oceny stabilności procesu, jednak przy ich tradycyjnym sposobie wykorzystywania (tzn. przy metodzie stabilizacyjnej i typowych granicach kontrolnych) nie pozwalają na jednoznaczną ocenę tego, czy proces jest realizowany zgodnie z wymaganiami klienta. Można sobie bowiem łatwo wyobrazić proces, który jest statystycznie ustabilizowany (powtarzalny) i przebiega w ramach obliczonych granic kontrolnych, a wytwarzane jest np. 90% wyrobów niezgodnych. I odwrotnie – proces może być bardzo nieustabilizowany, ale nie produkować wcale wyrobów niezgodnych (przy wystarczająco szerokich granicach tolerancji ustalonych przez klienta). Potrzebny jest zatem jakiś wskaźnik, który jednoznacznie będzie odnosił zmienność (rozrzut) procesu do zadanych granic tolerancji. W ramach statystycznego sterowania procesami wykorzystywanych jest kilka podstawowych wskaźników zdolności, które odnoszą się albo do zdolności całych procesów, albo tylko poszczególnych maszyn. Są one stosunkowo proste do wyznaczenia, ale wykorzystywane bez należytej uwagi mogą prowadzić do fałszywych wniosków.
Przy wykorzystywaniu do sterowania procesem karty kontrolnej, można odnosić otrzymywane wyniki do obliczonych granic kontrolnych i oceniać jego stabilność. Jak na karcie takiej zazwyczaj nie można nanosić granic tolerancji, co uniemożliwia ocenę jego zdolności do spełniania wymagań klienta. Chcąc ocenić zdolność procesu należy odnieść bezpośrednio jego rozrzut (szacowany zazwyczaj w oparciu o rozstęp lub odchylenie standardowe) do szerokości założonego pola tolerancji (rys. 1).
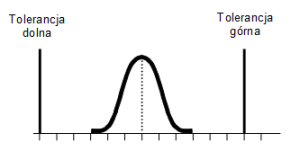
Rys. 1.Istota wyznaczania zdolności procesu
Im szerokość procesu jest mniejsza w odniesieniu do szerokości pola tolerancji tym proces jest bardziej zdolny. Zakładając, że „szerokość” procesu można wyrazić jako 6 odchyleń standardowych (założenie to jest właściwe dla rozkładu zgodnego z rozkładem normalnym, przy innych rozkładach stosuje się inne wzory), można skonstruować wzór na podstawowy wskaźnik oceny zdolności procesu nazywany Cp:
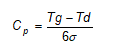
gdzie:
Tg – górna wartość tolerancji,
Td – dolna granica tolerancji,
s – odchylenie standardowe.
Jak można wywnioskować z konstrukcji tego wzoru, im wskaźnik ten ma wyższą wartość, tym lepszy proces (dla procesu przedstawionego na rysunku 1 wynosi on około 2). W przypadku, gdy wartość ta wynosi 1 (szerokość procesu jest równa zakresowi tolerancji), to zgodnie z własnościami rozkładu normalnego wadliwość wynosi 0,27%. W zależności od wymagań klienta może to być dużo lub mało. Ogólnoświatowym standardem jest tu wartość 1,33, przy której wadliwość wynosi około 0,0063%.
Przed rokiem 1980, który jest powszechnie uważany za początek stosowania na dużą skalę metod statystycznych w zarządzaniu jakością, wskaźniki Cp uzyskiwane w przeciętnych amerykańskich przedsiębiorstwach nie przekraczały wartości 0,67. W latach osiemdziesiątych ubiegłego wieku japończycy ustalili swoje standardy zdolności procesu na wartość 1,33 [1]. Wymagana wartość wskaźników zdolności jest obecnie uzależniona od branży. W przemyśle motoryzacyjnym wartością docelową jest np. 1,67.
Przedstawiony wzór na wartość Cp jest bardzo prosty i wręcz intuicyjny, jednak niestety niewystarczający do jednoznacznej oceny procesu. Proces może mieć bowiem „szerokość” mniejszą od przedziału tolerancji (np. Cp=2), ale np. 90% wyrobów niezgodnych, gdy jest przesunięty daleko poza pole tolerancji. Wskaźnik Cp nie reaguje bowiem na przesunięcie procesu (rys. 2).
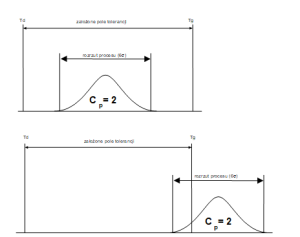
Rys. 2. Wartości wskaźnika Cp przy różnym położeniu procesu
W celu nadzorowania wycentrowania procesu wykorzystywany jest wraz z Cp drugi wskaźnik, oznaczany jako Cpk. Wskaźnik ten ma konstrukcję podobną do Cp, z tym, że uwzględnia wartość średnią procesu i oddzielnie ocenia zdolność obu „połówek” procesu. Oddzielnie wyznacza się zdolność procesu w odniesieniu do górnej i dolnej granicy tolerancji obliczając Cpkg i Cpkd (rys. 3). Wartość Cpk jest wartością mniejszą (czyli gorszą) z Cpkg i Cpkd.
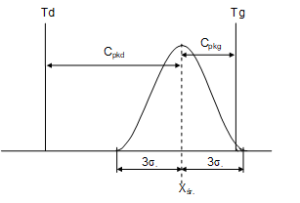
Rys. 3. Idea wyznaczania wskaźnika Cpk
Wzory wykorzystywane przy obliczaniu Cpk są następujące:
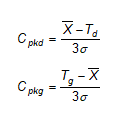
Jak można wywnioskować po przeanalizowaniu przedstawionych wzorów, wartość Cp może się zmieniać w zakresie (0,+∞). Wartość Cpk zmieniać się może w przedziale (-∞,+∞), przy czym jego wartość nie może nigdy przekroczyć wartości Cp dla danego procesu, czyli w praktyce będzie się on zmieniał w przedziale (‑∞,Cpñ. Wskaźniki Cp i Cpk będą sobie równe, gdy proces będzie położony dokładnie na środku pola tolerancji.
Na rys. 4 przedstawiono proces, którego zdolność potencjalna wynosi 1. Jeżeli proces ten jest wycentrowany w polu tolerancji, jego wadliwość wynosi 0,27%. Każde jednak przesunięcie procesu względem środka pola tolerancji powoduje gwałtowny wzrost liczby braków. Nie ma zatem marginesów bezpieczeństwa, pozwalających na sterowanie procesem i reagowanie na jego przesunięcie.
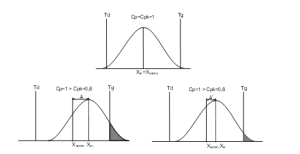
Rys. 4. Wartości wskaźników zdolności przy przesunięciu procesu
Przy procesie o zdolności potencjalnej 1,7 wycentrowanym w polu tolerancji, wadliwość wynosi około 0,0001%. Przesunięcie procesu oczywiście powoduje wzrost wadliwości, ale jest ona o wiele mniejsza, niż przy tym samym przesunięciu w przypadku procesu o Cp=1 (rys. 5).
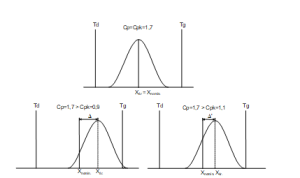
Rys. 5. Wartości wskaźników zdolności przy przesunięciu procesu
Sterując procesem należy zatem dążyć do jak najwyższych (oczywiście w granicach rozsądku, odnosząc to do kosztów i potrzeb klienta) wartości Cp i jak najmniejszej różnicy pomiędzy Cp i Cpk.
Stosowanie omawianych wskaźników może mieć miejsce tylko w przypadku oceny zdolności procesu, który jest statystycznie ustabilizowany. Wartości potrzebne do ich wyznaczenia to granice tolerancji (narzucane zwykle przez klientów), wartość średnia położenia procesu oraz odchylenie standardowe. W przypadku wskaźników Cp i Cpk odchylenie standardowe wyznacza się z wartości średniego rozstępu lub średniego odchylenia standardowego odczytanego z kart kontrolnych. Odchylenie procesu jest więc wyznaczane ze zmienności wewnątrzpróbkowej, dlatego spełnienie założenia o stabilności procesu jest tu bardzo ważne (wyznaczanie wskaźników Cp i Cpk dla procesu niestabilnego będzie skutkowało zawyżaniem zdolności).
Warto też zwrócić uwagę na to, że do wyznaczenia Cp potrzebne są wartości obu granic tolerancji. Gdy tolerancja jest jednostronna, obliczenie Cp jest niemożliwe, a zdolność procesu wyznacza się tylko przez obliczenie Cpk.
W tabeli 1 przedstawiono wadliwości procesów, dla wybranych wartości wskaźników Cp i Cpk.
Tabela 1. Poziom PPM (liczba wyrobów wadliwych na milion) dla wybranych wartości wskaźników zdolności
| Wskaźnik zdolności Cp | Wartość różnicy (Cp-Cpk) | ||||||
| 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | ||
| 0,5 | 133 614 | 151 000 | 201 924 | 282 451 | 385 556 | ponad 500 000 | |
| 1 | 2 700 | 3 950 | 8 357 | 17 912 | 35 943 | 66 810 | |
| 1,33 | 63 | 120 | 351 | 1 001 | 2 635 | 6 387 | |
| 1,67 | 1 | 1 | 5 | 20 | 69 | 224 | |
| 2 | 0 | 0 | 0 | 0 | 1 | 3 | |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | |
Firma nadzoruje jeden z realizowanych u siebie procesów produkcyjnych pobierając i mierząc co 2 godziny próbkę składającą się z trzech wyrobów. Wartość nominalną ustalono na 5,45 z obustronną tolerancją 0,25. Obliczona z pobranych 25 próbek wartość średnia procesu wynosi 5,58 – proces jest więc przesunięty w stronę tolerancji górnej. Średni rozstęp w zebranych próbkach (rozstęp to różnica pomiędzy największym a najmniejszym pomiarem) wynosi 0,085. Z rozstępu tego można po dobraniu z odpowiedniej tabeli (dostępnej w większości podręczników dotyczących metod statystycznych) wartości współczynnika d2 wyznaczyć odchylenie standardowe:
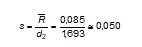
Graficznie sytuację tą można przedstawić tak jak na rys. 6.
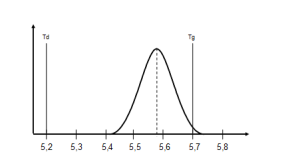
Rys. 6. Położenie badanego procesu w granicach tolerancji
Wskaźniki zdolności dla tego procesu (przy założeniu, że jest on procesem statystyczne ustabilizowanym oraz wyniki układają się zgodnie z rozkładem normalnym) wyniosą:
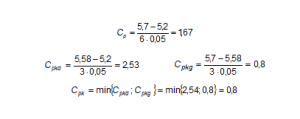
Proces jest zatem potencjalnie zdolny (wartość Cp jest dużo większa niż 1, wadliwość 1 PPM), ale jest bardzo przesunięty w kierunku tolerancji górnej, co powoduje znaczący wzrost liczby wyrobów niezgodnych z wymaganiami (8 198 PPM). W analizowanym przypadku należy tak zadziałać na proces, aby jego wartość średnia pokryła się z zakładanym nominałem (środkiem pola tolerancji). Nie trzeba jednak podejmować działań zmniejszających rozrzut procesu (co jest działaniem o wiele trudniejszym i zwykle droższym niż przesunięcie średniej procesu).
Opisane wskaźniki mogą być wyznaczane na podstawie przedstawionych wzorów przy spełnieniu kilku bardzo ważnych założeń:
Spełnienie tych założeń jest podstawą uzyskania wiarygodnych danych na temat ocenianego procesu. Przed rozpoczęciem obliczeń z wykorzystaniem przedstawionych powyżej wzorów należy zatem wybraną metodą sprawdzić zgodność rozkładu z rozkładem normalnym, a za pomocą np. karty kontrolnej ocenić stabilność procesu.
Jak już zaznaczono wcześniej, stosowanie standardowych wskaźników Cp i Cpk możliwe jest w odniesieniu do procesów statystycznie ustabilizowanych. W przypadku, kiedy warunek ten nie jest spełniony, proces ocenia się dzięki wskaźnikom Pp i Ppk. Wzory pozwalające na ich obliczenie są identyczne jak w przypadku wskaźników Cp i Cpk. Różnica przy obliczaniu wartości tych wskaźników polega jedynie na innym sposobie wyznaczania odchylenia standardowego. Tu oblicza się je uwzględniając wszystkie pojedyncze pomiary (a nie tylko np. średni rozstęp) wykorzystując wzór:
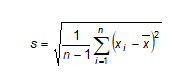
W przypadku wskaźników Pp i Ppk nadal obowiązuje założenie normalności rozkładu zebranych wyników pomiarów, ale proces nie musi być już ustabilizowany. Wskaźniki te są stosowane także na początku sterowania procesem, kiedy nie wiadomo jeszcze, czy jest on stabilny.
Na rys. 7 przedstawiono kartę kontrolną X-R przykładowego procesu, który nie jest procesem stabilnym (występują punkty poza granicami kontrolnymi).
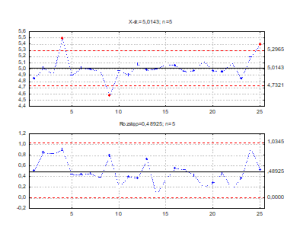
Rys. 7. Karta X-R procesu niestabilnego
Przy założeniu, że dla przedstawionego procesu tolerancje ustalono jako 5±0,7, wskaźnik Cp=0,95, a wskaźnik Pp=0,77. Różnica jest więc znaczna, a stosowanie wskaźnika Cp dla procesu niestabilnego znacząco zawyża jego zdolność.
Cztery podstawowe wskaźniki służące do oceny procesu są stosunkowo proste do obliczenia, ale mają co najmniej dwie podstawowe wady:
Najpoważniejszą wadą wskaźników Cpk i Ppk jest to, że ich wartość określa tylko wadliwość procesu od strony tolerancji, której bliżej jest wartość średnia procesu. Bardzo dobrze można to przedstawić analizując wyniki oceny zdolności za pomocą wskaźników Cp i Cpk następujących dwóch procesów:
Wskaźniki zdolności dla tych procesów są następujące:
Z wartości tych wynika, że lepszą zdolność potencjalną ma proces B, ale jest on przesunięty w polu tolerancji i wskaźnik jego zdolności Cpk jest niższy niż przy procesie A. Niższa wartość Cpk sugeruje, że wadliwość jest większa. I faktycznie jest większa, ale tylko wadliwość jednostronna (w odniesieniu do tolerancji górnej). Wadliwości obustronne są następujące (rys. 8):
Patrząc ogólnie, proces B jest więc procesem lepszym i to z dwóch powodów. Pierwszy to oczywiście jego mniejsza sumaryczna wadliwość. Drugą ważną przewagą procesu B jest jego zdecydowanie mniejszy rozrzut w odniesieniu do tolerancji niż w przypadku procesu A. O wiele łatwiej jest bowiem zazwyczaj poprawić wartości wskaźnika Cpk (wystarczy bowiem „tylko” przesunąć wartość średnią procesu, np. przez przestawienie maszyny), niż zmniejszyć rozrzut procesu, co zwiększy wartość Cp (wymaga to zwykle zmiany technologii, zakupu bardziej precyzyjnych maszyn itp.).
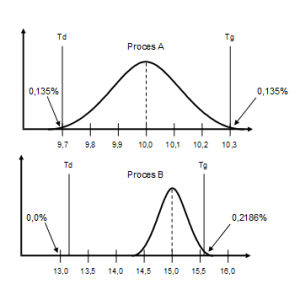
Rys. 8. Procesy A i B – porównanie zdolności
Podsumowując należy więc wyraźnie zaznaczyć, że ani wartość Cp ani Cpk (ani ich odpowiedniki Pp i Ppk) nie odnoszą się bezpośrednio do wadliwości procesu. Wskazują one jedynie na potencjalną (Cp i Pp), bądź jednostronną zdolność (Cpk i Ppk) i dopiero uważna analiza obu wskaźników (właściwych z uwagi na stabilność procesu) na raz może dostarczyć właściwych informacji o procesie.
W przypadku granic tolerancji niesymetrycznych względem nominału, opisane wskaźniki nie będą informowały o przesunięciu wartości średniej procesu. Zazwyczaj pożądane uzyskanie równości wskaźników Cp i Cpk tutaj będzie objawem nieprawidłowego przebiegu procesu (poniżej lub powyżej nominału). Pewnym rozwiązaniem, chociaż nie idealnym, może tu być wykorzystanie wskaźnika zdolności uwzględniającego wartość nominalną, który jest oznaczany jako Cpm.
Wskaźnik Cpm wprowadzili Chan, Cheng i Spiring [2], jako wskaźnik stosowany zamiast lub oprócz standardowych wskaźników Cp i Cpk. Wskaźnik ten wyznaczany jest ze wzoru:

gdzie:
T – wartość nominalna,
s – odchylenie standardowe.
Jak wynika z przedstawionego wzoru, na wartość mianownika wpływa nie tylko odchylenie standardowe zebranych wyników pomiarów określonej właściwości wyrobu, ale także przesunięcie średniej procesu względem wartości nominalnej. Przy określonym odchyleniu standardowym, wartość wskaźnika Cpm jest największa, gdy średnia procesu pokrywa się z nominałem. Im jest ona dalej od nominału, tym mniejsza wartość wskaźnika.
Na rys. 9 przedstawiono proces wycentrowany w granicach tolerancji, Ponieważ wartość średnia pokrywa się z nominałem, a nominał pokrywa się ze środkiem pola tolerancji, wszystkie trzy wartości wskaźników są sobie równe. Wadliwość procesu jest mała (0,0006%), a w przedziale jednego odchylenia standardowego wokół nominału znajduje się około 68% wyników.
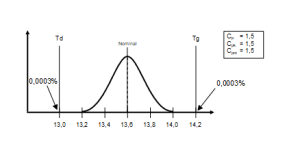
Rys. 9. Proces wycentrowany, zgodny z nominałem
Na rys. 10 przedstawiono proces potencjalnie zdolny, ale przesunięty względem nominału i środka pola tolerancji. Wadliwość w tym procesie wynosi 0,135% (co w pewnym sensie sygnalizuje wartość wskaźnika Cpk), ale wokół nominału (w przedziale jednego odchylenia standardowego) znajduje się tylko około 30,1%, czyli ponad dwa razy mniej niż przy procesie wycentrowanym. Problem z dotrzymaniem nominału sygnalizowany jest przez Cpm.
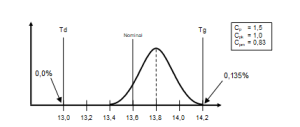
Rys. 10. Proces przesunięty względem tolerancji i nominału
Na kolejnym rysunku (rys. 11) przedstawiono proces w części wyraźnie przesunięty poza granicę tolerancji, dla którego wadliwość wynosi około 6,83%. Proces ten jest dodatkowo przesunięty daleko względem wartości nominalnej, przez co liczba wyników wokół nominału jest znikoma.
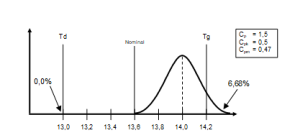
Rys. 11. Proces przesunięty względem tolerancji i nominału
Na rys. 12 przedstawiono proces o wadliwości 50%, dla którego wartość średnia pokrywa się z tolerancją. Potencjalna zdolność procesu jest nadal wysoka, ale jak wskazuje wskaźnik Cpk, połowa procesu jest poza polem tolerancji (przy procesie „szerokim” będzie to oczywiście informacja, że co najmniej połowa procesu przekracza jedną z tolerancji, ponieważ druga strona procesu też może się w tolerancji nie zmieścić w całości).
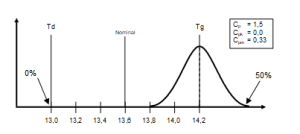
Rys. 12. Proces ze średnią na wartości tolerancji górnej
Proces z niesymetrycznymi granicami tolerancji względem wartości nominalnej przedstawiono na rys. 13. Jak widać wskaźniki Cp i Cpk wskazują na wysoką zdolność procesu, ale wskaźnik Cpm informuje o przesunięciu procesu względem nominału. Wadliwość tego procesu wynosi 0%, ale wokół nominału znajduje się tylko około 2% wyników.
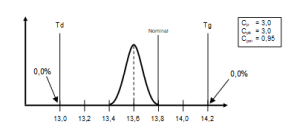
Rys. 13. Proces z niesymetrycznymi granicami tolerancji
W przypadku przedstawionym na rys. 14 proces jest wprawdzie przesunięty w polu tolerancji, ale za oto jego wartość średnia pokrywa się z założonym nominałem. Wskaźnik Cpk wskazuje zatem na przesunięcie procesu, a równość Cp i Cmk świadczy o zgodności średniej procesu z nominałem (wokół nominału znajduje się około 68% wyników). Wskaźnik Cpm dobrze więc obrazuje dokładność procesu (w odniesieniu do założonego nominału).
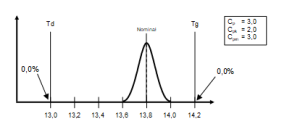
Rys. 14. Proces z niesymetrycznymi granicami tolerancji
Niestety, gdyby dla przedstawionego powyżej procesu wartość nominalna wynosiła np. 14,1, a średnia dokładnie by się z nią pokryła, wskaźniki Cp i Cpm nadal wskazywałyby na wysoką zdolność procesu (byłyby równe 3). W rzeczywistości jednak w procesie pojawiłoby się ponad 6% wyników poza tolerancjami. Widać tu wyraźną słabość wskaźnika Cpm, który zdolność procesu odnosi tylko do szerokości pola tolerancji i „odległości” średniej od nominału, a nie uwzględnia zbliżenia średniej procesu do granic tolerancji. Przy potencjalnie zdolnym procesie, przesuniętym bardzo blisko granicy tolerancji i położonym na wartości nominalnej wskaźnik Cpm nie będzie sygnalizował pojawiającej się dużej wadliwości.
Naturalną potrzebą było więc opracowanie wskaźnika, którego wartość zależałaby zarówno od przesunięcia średniej procesu względem wartości nominalnej, jak i odległości tej średniej od założonych granic tolerancji. Wskaźnik taki zaproponowali w roku 1992 Pearn, Kotz i Johnson [3]. Ma on postać:
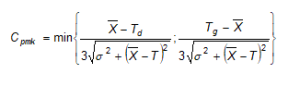
Na rys. 15 przedstawiono omówiony już wcześniej proces, dla którego wartość średnia pokrywa się z wartością nominalną przy niesymetrycznych granicach tolerancji oraz to jak zmienią się wartości wskaźników, gdy wartość nominalna będzie ustalona bardzo blisko granicy tolerancji. Jak widać wskaźniki Cp oraz Cpm wskazują na wysoką zdolność procesu. Dopiero wskaźnik Cpk, informuje, że proces „wystaje” przynajmniej jednostronne poza granice tolerancji. Po analizie wartości wskaźnika Cpmk, którego wartość jest mniejsza niż Cpk, można wyciągnąć kompletny wniosek o zachowaniu się procesu: nie mieści się on w granicach tolerancji, a dodatkowo jest przesunięty względem nominału.

Rys. 15. Wyniki oceny zdolności z wykorzystaniem Cpmk
Wskaźnik ten może być uznany za najlepszy z przedstawionych, gdyż uwzględnia najwięcej czynników rzutujących na faktyczną jakość procesu (zarówno rozrzut procesu jak i jego odniesienie do wartości nominalnej). Jest on jednak dosyć trudny w interpretacji i w praktyce rzadko stosowany.
W przypadku, gdy rozkład danych nie jest zgodny z rozkładem normalnym, można zastosować jedno z dwóch podstawowych rozwiązań. Pierwsze z nich polega na wykorzystaniu krzywych Johnsona, które pozwalają na przekształcenie „otrzymanego rozkładu” do postaci standaryzowanego rozkładu normalnego. Drugie wymaga ogólnej znajomości charakterystyki „otrzymanego” rozkładu i wyznaczenia takiej wartości mierzonej własności A, poniżej której znajduje się 0,135% pomiarów, a następnie wartości B, powyżej której znajduje się 0,135%, czyli poniżej którego 99,865% (jest to wyznaczanie tzw. percentyli). Różnicę B-A traktuje się jako 6s przy rozkładzie normalnym i wstawia do mianownika omówionych wzorów (rys. 16).

Rys. 16. Sposób wyznaczania przedziału 6 dla rozkładu normalnego i innego niż normalny
Postępowanie takie jest oczywiście pracochłonne i stosowane właściwie wyłącznie w przypadku możliwości skorzystania z odpowiedniego oprogramowania komputerowego.
Bez wątpienia wskaźniki zdolności są nieodzownym elementem sterowania procesami, szczególnie procesami produkcyjnymi. Praktycznie nie jest możliwe, aby bez ich wykorzystania doprowadzić nadzorowane procesy do takiego stanu, aby w sposób optymalny (i możliwie oszczędny) spełniały potrzeby klientów. Należy jednak pamiętać, że nieumiejętne ich stosowanie może nie tylko nie pomóc w nadzorowaniu procesu, ale wręcz ten proces rozregulować. Warto więc pomyśleć skąd biorą się te, wyznaczane zazwyczaj przez różne programy komputerowe, wskaźniki i jak je interpretować, żeby faktycznie stały się orężem w walce z brakami.
Autor: Tomasz Greber [PROQUAL]
Literatura
Szkolenia otwarte
Szkolenia zamknięte
PROQUAL Management Institute
B. T. Greber Spółka Jawna